Lab 3: FPGA Video Controller and Sound Generation

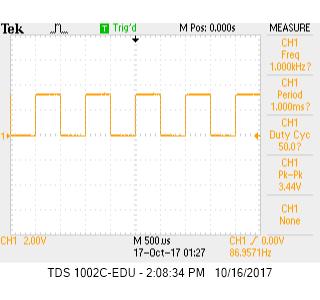
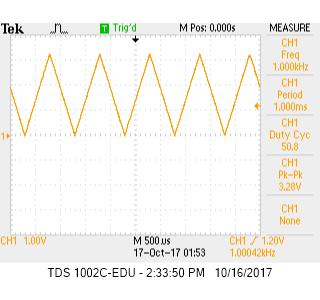
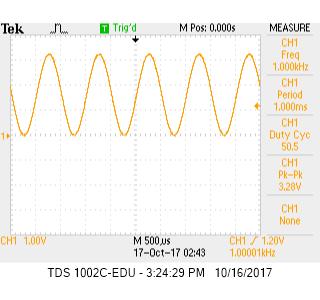
Team Members

• Nicolas Casazzone
• Alicia Coto
• Raul Pacheco

Materials

• Arduino Uno
• FPGA DE0_nano
• 8-bit DAC Connector
• VGA Cable
• Various Resistors
• 2x Switches

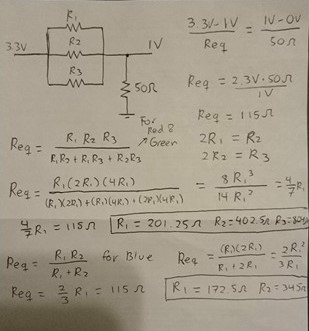
Deciding Resistor Values for the 8-bit DAC

To encode colors to the screen, we needed to use an 8-bit DAC (Digital to Analog Converter), which is shown in the image below. This DAC uses 3 of the bits to encode the values for the color red, 3 bits to encode green, and 2 bits to encode blue. This DAC connects to 8 pins on the FPGA that then feeds through 8 different resistors. From there, the group of wires for each color combine to produce a voltage between 0 and 1 V. The resistors step down the voltage from 3.3 volts to different voltages. The resistor values for each resistor in a color group must correspond with different voltage step downs so that a range of out voltages can be attained. For red and green, since they are comprised of 3 bits, 8 different colors should be producible. This means that 8 different voltages between 0 and 1V should be achieved, each 1/7 of a volt apart.

From the picture above, each color indicated by R, G, B has resistors in parallel along with the VGA cable having a 50Ω resistance in series. The voltage of each color pin needs to sum to a total of 1V with each pin representing a bit. The most significant bit is twice the voltage of the second most significant bit, four times the voltage of the third most significant bit, and so on. The voltage of each color branch is 4/7V, 2/7V, and 1/7V respectively to the most significant bit order. Below is our worked out solution to finding the resistor values for the DAC. To keep the current across the resistors the same, the resistor for the most significant bit would be have twice the resistance of the second significant bit, and so on, just like the voltages. Hence the assumption of 2R1=R2, and 2R2=R3.

Drawing to the Screen

We were given a VGA module written in verilog that is used to write values to the pixels on our screen. The module works with our main module by giving it an x and y coordinate (PIXEL_COORD_X and PIXEL_COORD_) that correspond to the position of a pixel on the screen. In the main module, we write a color to the pixel in an 8 bit variable, PIXEL_COLOR, which is then sent by the VGA driver to the DAC and eventually displays the color on the screen. The first 3 bits of PIXEL_COLOR coorespond to red, the next 3 to green and the last two to blue. The VGA module incrememnts through each pixel on the screen by continuously outputting the next pixel coordinates. In the image below, every pixel was assigned to green (8'b000_111_00).

External Inputs to the Screen

Before using external imputs we first wanted to create a 2x2 grid on the screen. The code below shows the logic that we used. We used a 2x2 matrix, my_grid of 8 bit values to store the colors of each sqare in the grid. The 1 bit regs, newx and newy, convert PIXEL_COORD_X and PIXEL_COORD_Y into values that correspond to each box in the 2x2 grid. If x is 0, we are assigning to the column on the left; if x is 1, we are assigning to the column on the right. If y is 0 we are assigning to the top row, if y is 1, we are assigning to the bottom row. We made our grid 200 pixels by 200 pixels so we added a case for if the pixel was located beyond our grid. If it was, it was simply assigned the color black, which is 8 zeros. This allows us to assign PIXEL_COLOR to the value stored in my_grid[x][y]. The always block used with an asterix ensures that the block runs whenever any input signal changes.

                         wire[7:0] my_grid[1:0][1:0];
 
                         reg newx;
                         reg newy;
                         
                         assign my_grid[0][0] = 8'b000_000_11;
                         assign my_grid[1][0] = 8'b111_111_11;
                         assign my_grid[0][1] = 8'b111_111_11;
                         assign my_grid[1][1] = 8'b000_000_11;

                        always @ (*) begin 
     
                            newx = PIXEL_COORD_X/10'd100;
                            newy = PIXEL_COORD_Y/10'd100;
                            if (PIXEL_COORD_X > 199 | PIXEL_COORD_Y > 199) begin
                                PIXEL_COLOR = 8'd0;
                            end
                            else begin
                                PIXEL_COLOR = my_grid[newx][newy];
                            end
                        end
                        

In order to demonstrate an external input controlling our 2x2 grid, we implemented two switches to provide combinations for our four possible grid outcomes. The switch has 3 pins, only two of which are connected at a time. We made the middle pin the signal pin with the two other pins being 3.3 volts and ground. When the switch is flipped, the signal pin flips between 0 and 3.3 volts. This is read as a 0 or 1 by the FPGA. The following image shows how we wired the switches to pins on the FPGA.

Each different switch position combination corresponds with a blue box being in one of the 4 quadrants of our grid. The table below shows the different outputs based on the switch position.

Switch One	Switch Two	Blue Quadrant
0	0	Top Left
1	0	Top Right
0	1	Bottom Left
1	1	Bottom Right

Below is our code which uses the switch inputs to determine the color of each quadrant of my grid. Pin1 and pin2 were assigned to the GPIO pin that the switch signal was plugged into on the FPGA.

                         always @ (*) begin 
                            if(pin1 == 0 & pin2 == 0)begin
                                 my_grid[0][0] <= 8'b000_000_11;
                                 my_grid[1][0] <= 8'b111_111_11;
                                 my_grid[0][1] <= 8'b111_111_11;
                                 my_grid[1][1] <= 8'b111_111_11;
                             end 
                             else if(pin1 == 1 & pin2 == 0)begin
                                 my_grid[0][0] <= 8'b111_111_11;
                                 my_grid[1][0] <= 8'b000_000_11;
                                 my_grid[0][1] <= 8'b111_111_11;
                                 my_grid[1][1] <= 8'b111_111_11;
                             end
                             else if(pin1 == 0 & pin2 == 1)begin
                                 my_grid[0][0] <= 8'b111_111_11;
                                 my_grid[1][0] <= 8'b111_111_11;
                                 my_grid[0][1] <= 8'b000_000_11;
                                 my_grid[1][1] <= 8'b111_111_11;
                             end
                             else begin
                                 my_grid[0][0] <= 8'b111_111_11;
                                 my_grid[1][0] <= 8'b111_111_11;
                                 my_grid[0][1] <= 8'b111_111_11;
                                 my_grid[1][1] <= 8'b000_000_11;
                             end
                             
                             
                            newx = PIXEL_COORD_X/10'd100;
                            newy = PIXEL_COORD_Y/10'd100;
                            if (PIXEL_COORD_X > 199 | PIXEL_COORD_Y > 199) begin
                                PIXEL_COLOR = 8'd0;
                            end
                            else begin
                                
                                PIXEL_COLOR = my_grid[newx][newy];
                            end
                        end
                        

Below is a video of our switches in action!

Team Members

• Ben Roberge
• Ryan Hornung

Goal

Our task was to first generate two or three different waveforms in Verilog and play them on the lab speakers via the stereo phone jack socket and the 8-bit R2R DAC. We chose to generate a 1 kHz square wave, a 1 kHz triangle wave, and a 1 kHz sine wave. After deciding which of the three sounded the best, we needed to create a short tune of at least three different frequencies, using our chosen waveform. Finally, we had to ensure we could turn our sound on or off using an enable signal.

Materials

• Arduino Uno
• FPGA DE0_nano
• Lab Speaker
• 8-bit R2R DAC
• Stereo phone jack socket

Square Wave

We began by synthesizing a simple square wave using the FPGA board. Because the signal is either high (3.3 V) or low (0 V), we can simply toggle the value of a GPIO pin. Below are the lines of code which we added to DEO_NANO.v.

                            localparam HALF_CYLCE = (25000000/1000)/2;

                            reg tone_1000;
                            reg [15:0] counter;
                            assign GPIO_0_D[0] = tone_1000;

                            always @ (posedge CLOCK_25) begin
                                if (reset) begin
                                    counter == 0
                                if (counter == 0) begin
                                    tone_1000 <= ~tone_1000;
                                    counter <= HALF_CYCLE - 1;
                                end
                                else begin
                                    tone_1000 <= tone_1000;
                                    counter <= counter - 1;
                                end
                            end
                        

First, we began by defining a local parameter called HALF_CYCLE. This parameter represents the number of clock cycles in a halve cycle of our square wave. In order to synthesize a 1 kHz square wave, the HALF_CYCLE will be the clock frequency divided by the desired frequency, and lastly divided by two (half). We also defined a couple of registers. First, counter is a 16-bit counter used to keep track of the number of clock cycles since the last signal edge. The register tone_1000 holds the output value of the square wave. Lastly, for the setup, we assigned the output pin GPIO_0_D[0] to the tone_1000 register.

Next, on each positive edge of the clock tick, we check the value of the counter. If the counter has reached zero, we negate the value in the tone_1000 register, and reset the clock to HALF_CYCLE - 1. Otherwise, the tone_1000 register is kept at its current value, and the counter is decremented. Toggling the tone_1000 output in this fashion allows us to create the 1 kHz square waveform. Below is the waveform of the square wave we generated.

Since our square wave is output as a one-bit signal, we did not need to use the 8-bit R2R DAC to play our square wave on the speaker. We simply connected the output from pin GPIO_0_D[0] to one of the input pins on the stereo phone jack socket, which connected directly to the speaker.

Triangle Wave

Now, we wanted to generate a slightly more complicated waveform, and we decided to make a 1 kHz triangle wave. In order to accomplish this, we added the following code to DEO_NANO.v:

                            reg [7:0] tri_1000;     // 1 kHz triangle wave
                            reg [5:0] tri_counter;
                            reg Incr;                // Increasing/decresing state variable
                            
                            assign GPIO_0_D[22] = tri_1000[0];
                            assign GPIO_0_D[20] = tri_1000[1];
                            assign GPIO_0_D[18] = tri_1000[2];
                            assign GPIO_0_D[16] = tri_1000[3];
                            assign GPIO_0_D[14] = tri_1000[4];
                            assign GPIO_0_D[12] = tri_1000[5];
                            assign GPIO_0_D[10] = tri_1000[6];
                            assign GPIO_0_D[8] = tri_1000[7];
                            
                            //State machine for 1 kHz triangle wave output
                            always @ (posedge CLOCK_25) begin
                                if (reset) begin
                                    Incr <= 1;
                                    tri_1000 <= 0;
                                    tri_counter <= 0;
                                end
                                if (tri_counter == 0) begin
                                    if ((Incr == 1) && (tri_1000 < 254)) begin
                                        Incr <= Incr;
                                        tri_1000 <= tri_1000 + 1;
                                        tri_counter <= 48;
                                    end
                                    else if ((Incr == 1) && (tri_1000 == 254)) begin
                                        Incr <= ~Incr;
                                        tri_1000 <= tri_1000 + 1;
                                        tri_counter <= 48;
                                    end
                                    else if ((Incr == 0) && (tri_1000 > 1)) begin
                                        Incr <= Incr;
                                        tri_1000 <= tri_1000 - 1;
                                        tri_counter <= 48;
                                    end
                                    else begin
                                        Incr <= ~Incr;
                                        tri_1000 <= tri_1000 - 1;
                                        tri_counter <= 48;
                                    end
                                end
                                else begin
                                    tri_1000 <= tri_1000;
                                    tri_counter <= tri_counter - 1;
                                end
                            end
                        

First, we declared an 8-bit register called tri_1000 to store the value of our triangle wave. Since it's 8-bits, tri_1000 can hold any value from 0 to 255. We once again made use of a decrementing counter, storing its value in the register tri_counter. The register Incr is used to keep track of whether the triangle wave's value is in an increasing or decreasing state. We then assigned the 8 bits of tri_1000 to output on 8 adjacent GPIO pins on the FPGA DE0_nano.

To actually create the triangle wave, we implemented a state machine. At each positive edge of the 25 MHz clock, we check the value of tri_counter. If tri-counter equals 0, there are four possible sets of commands. First, if tri_1000 < 254 and Incr equals 1 (indicating the increasing state), Incr needs to stay at 1, tri_1000 needs to increment, and tri_counter needs to be reset up to its maximum value. Second, if tri_1000 equals 254 and Incr equals 1, tri_1000 needs to increment up to 255 (its maximum value), Incr needs to flip to 0 (to start decreasing tri_1000's value when the counter next hits 0), and tri_counter needs to be reset up to its maximum value. Third, if tri_1000 > 1 and Incr equals 0 (indicating the decreasing state), Incr needs to stay at 0, tri_1000 needs to decrement, and tri_counter needs to be reset up to its maximum value. Fourth, if tri_1000 equals 1 and Incr equals 0, tri_1000 needs to decrement down to 0 (its minimum value), Incr needs to flip to 1 (to start increasing tri_1000's value when the counter next hits 0), and tri_counter needs to be reset up to its maximum value. Finally, if tri_counter does not yet equal 0, we simply keep the value of tri_1000 the same and decrement tri_counter.

It is important to note that we reset the value of tri_counter to 48 in order to achieve the proper wave frequency. For a 1 kHz wave, (25 MHz)/(1 kHz) = 25,000 clock cycles per wave period. For every wave period, the value of tri_1000 increments up 255 steps and decrements down 255 steps. Therefore, there are 510 steps per wave period. (25,000 cycles/period)/(510 steps/period) = 49 clock cycles per step. Setting tri_counter to 48 on the first clock cycle ensures that its value will be 0 on the 49th clock cycle. This is how we settled on the reset value of 48.

Before playing our triangle wave on our speaker, we checked the waveform using an oscilloscope. The output was exactly as we expected, a 1 kHz triangle wave with peak-to-peak voltage of 3.3V:

The picture below shows how we then connected the output from the FPGA to the speaker. The 8 GPIO pins that the 8 bits of tri_1000 are output on are connected to the 8 input pins on the 8-bit R2R DAC. The output pin on the R2R DAC then connects to one of the input pins on the stereo phone jack socket, which directly connects to the speaker.

Sine Wave

In order to generate a sine wave, we used a technique called direct digital synthesis (DDS). Prior to the program execution, a series of sine values are stored in memory which is then used as a lookup table for the output register. We began by generating 256 sine values using a simple python script. The below code creates a text file containing 256 sine values, spread over one period, each separated by a newline.

                            import math

                            def main():
                                values = []
                                for i in range(256):
                                    rad = 2.0 * math.pi * i / 256
                                    val = int(math.sin(rad) * 127) + 127
                                    values.append(val)
                                with open('sin_init.txt', 'w') as f:
                                    for val in values:
                                        f.write('{0:08b}\n'.format(val))
                                return

                            if __name__ == '__main__':
                                main()
                        

In order to store these values on the FPGA, we used the readmemb() function which takes in the text file and places the data memory. In order to actually step through the sine table, we utilized a 32 bit accumulator. The top 8 bits of this accumulator where used as an index into the sine table. How fast we increment the accumulator is dependant on the frequency of the sine wave. The increment is calculated by taking the maximum 32 bit number (2^32), dividing by the clock frequency and multiplying by the frequency of the sine wave. On each positive edge of the clock, we increment the accumulator by the calculated amount, and output the value from the sine table. When the accumulator overflows, it will simply roll over to 0 and begin stepping through the sine table again. Below is the code we used to generate a 1 kHz sine wave along with the corresponding waveform.

                            input CLK;
                            input RESET;

                            reg  [31:0] phase_accumulator;
                            reg  [31:0] phase_increment;

                            output reg [7:0] SOUND;

                            reg [7:0] rom[7:0];

                            initial
                            begin
                                $readmemb("sin_init.txt", rom);
                            end
                                
                            always @(posedge CLK) begin
                                if (RESET) begin
                                    phase_accumulator = 0;
                                    phase_increment = (2**32 / 25000000) * 1000;
                                end
                                else begin
                                    phase_accumulator = phase_accumulator + phase_increment;
                                    SOUND = rom[phase_accumulator[31:24]];
                                end
                            end
                        

In the same manner as for the triangle wave, we connected this sine wave output to the speaker via the 8-bit R2R DAC and the stereo phone jack socket.

Multiple Tones

After listening to our square wave, triangle wave, and sine wave tones, we decided to make the multiple- frequency tone using different frequency sine waves because the sine wave sounded the best of the three. In order to generate a signal with multiple tones, we created another array in memory to keep the increment variables for various frequencies. On each positive edge of the clock tick, we increment a counter. Once this counter reaches the number of cycles which equal one second, we move to the next tone in the array. All we have to do to move to the next tone is update the current phase_increment variable and reset the counter and accumulator. In addition to the multiple tones, you can toggle the playing of the sound using switch 1 on the FPGA board. Below is the code we added to generate multiple tones.

                            localparam ONE_SEC = 25000000; // one second in 25MHz clock cycles

                            input [1:0] SW;

                            reg [32:0] tones[3:0];
                            reg [24:0] time_counter;
                            reg [1:0] tone_counter;

                            reg [7:0] rom[2**8-1:0];

                            initial
                            begin
                                $readmemb("sin_init.txt", rom);
                                tones[0] <= 75591; // 440 Hz
                                tones[1] <= 151182; // 880 Hz
                                tones[2] <= 302365; // 1760 Hz
                                tones[3] <= 151182; // 880 Hz
                            end
                                
                            always @(posedge CLK) begin
                                if (RESET) begin
                                    time_counter = 0;
                                    tone_counter = 0;
                                    phase_accumulator = 0;
                                    phase_increment = tones[tone_counter]; // 1 kHz
                                end
                                if (~SW[1]) begin
                                    if (time_counter == ONE_SEC) begin
                                        time_counter = 0;
                                        tone_counter = tone_counter + 1;
                                        phase_accumulator = 0;
                                        phase_increment = tones[tone_counter];
                                        phase_accumulator = phase_accumulator + phase_increment;
                                        SOUND = rom[phase_accumulator[31:24]];
                                    end
                                    else begin
                                        phase_accumulator = phase_accumulator + phase_increment;
                                        SOUND = rom[phase_accumulator[31:24]];
                                        time_counter = time_counter + 1;
                                    end
                                end
                                else begin
                                    time_counter = 0;
                                    tone_counter = 0;
                                    phase_accumulator = 0;
                                    phase_increment = tones[tone_counter]; // 1 kHz
                                end
                            end
                        

Below are two videos showing the functionality of our code. The first video is simply our three tone signal playing continuously. The second video shows the signal being toggled on and off using switch 1 on the FPGA board.